The emergence of new modalities such as Diffusion Tensor Imaging (DTI) is of great interest for the characterization and the temporal study of Multiple Sclerosis (MS). DTI indeed gives information on water diffusion within tissues and could therefore reveal alterations in white matter fibers before being visible in conventional MRI. However, recent studies generally rely on scalar measures derived from the tensors such as FA or MD instead of using the full tensor itself. Therefore, a certain amount of information is left unused. Moreover, many sources can result in a bias in the images, for example errors in non linear registration or artifacts or distortion in the acquisitions. This bias may therefore lead to a prejudice in the results of any statistical analysis.

A. Atlas Construction for DTI White Matter Differences Detection

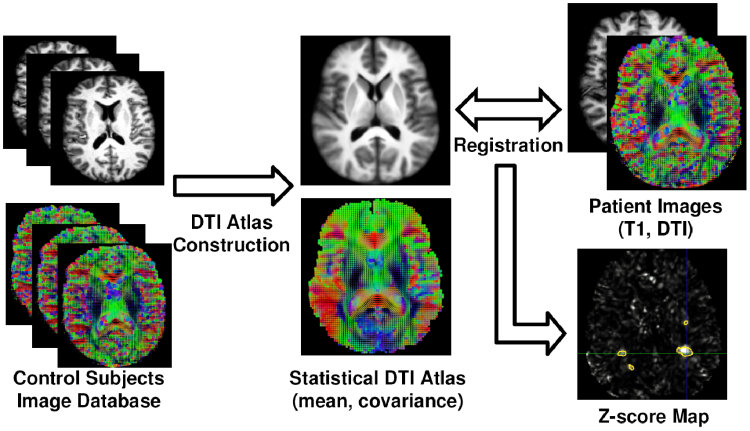
We have presented in [2] a framework to study the benefits of using the whole diffusion tensor information to detect statistically significant differences between each individual MS patient and a database of control subjects. This framework is based on the construction of a mean DTI atlas built from the control subjects in the following manner:

• Construction of an average T1 image (atlas) from the database of control subjects
• Application of the transformations to the DTI images
• Construction of the DTI atlas (mean and covariance of tensors)

The mean \( \bar{D}_{\mathrm{Log}} \) and covariance \( C \) of the tensors in each voxel can conveniently be computed in a vector space thanks to the Log-Euclidean framework for tensors proposed by Arsigny et al [1]. Once this DTI atlas has been built, each of the MS patient DTI is then compared with respect to it by utilizing the following approach, illustrated in Fig. 1:

• Non linear registration of the T1 image of the patient on the atlas
• Application of the transformation to the patient's DTI
• Computation of the Mahalanobis distance at each voxel using the values of the DTI atlas
• Derive p-values from these Mahalanobis scores

Figure 1: Overall scheme of patient to atlas DTI comparison.

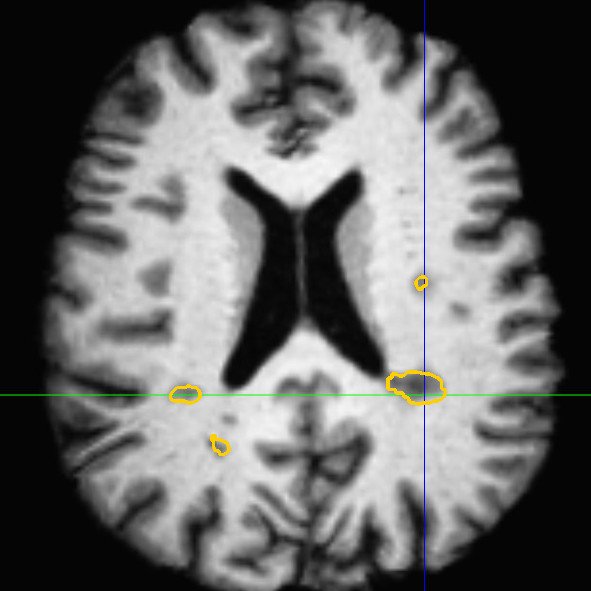
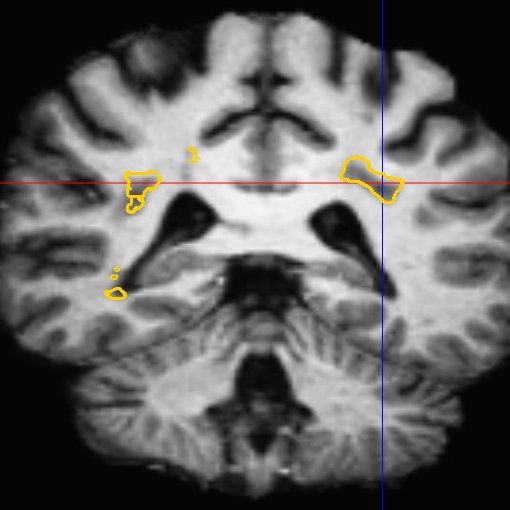
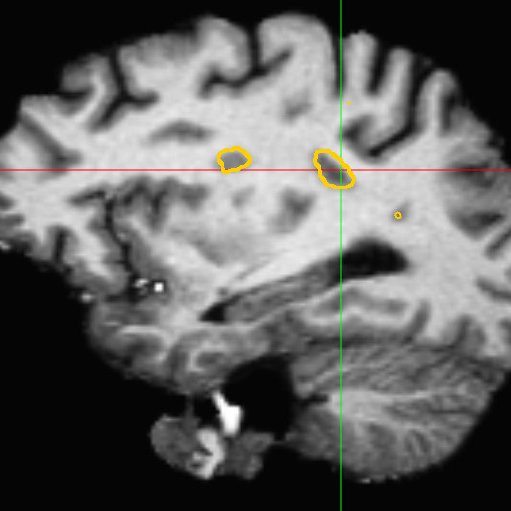
This framework allows us to look for differences both in normally appearing white matter but also in and around the lesions of each patient. We have presented in [2] a study on a database of 11 MS patients (one result example is shown in Fig. 2), showing the ability of the DTI to detect not only significant differences on the lesions but also in regions around them, enabling an early detection of an extension of the MS disease.

Figure 2: Voxel-wise z-scores for a given MS patient. Illustration of the z-score maps obtained for a patient (images (d), (e), (f)) compared to the corresponding anatomy (axial (a),(d), coronal (b),(e) and sagittal slices (c),(f)). The contours correspond to the manual delineations of the MS lesions.

(a)	(b)	(c)
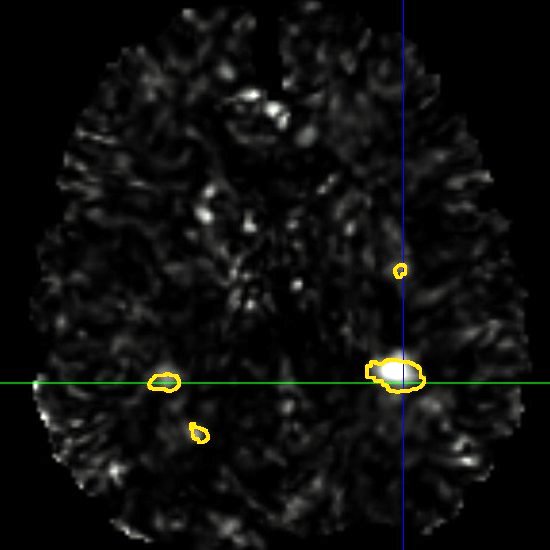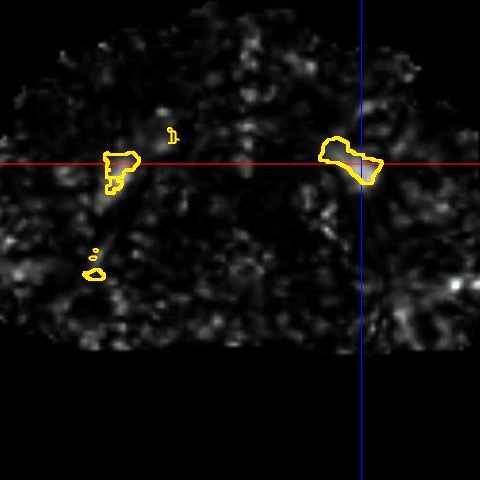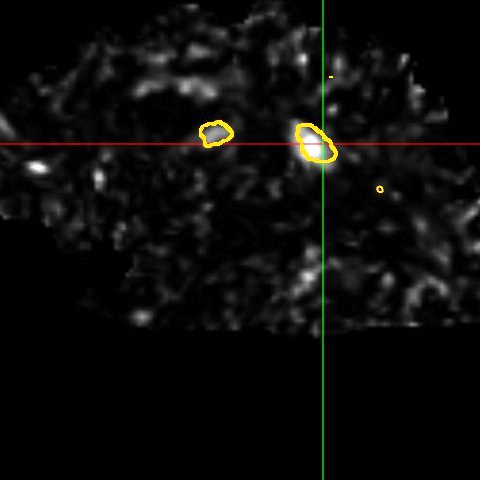(d)	(e)	(f)

B. Introducing Robustness in the Comparison: A continuous STAPLE on Vector Images

As mentioned previously, many sources can result in a bias in the images, for example errors in non linear registration or artifacts or distortion in the acquisitions. This bias may therefore lead to a prejudice in the results of any statistical analysis. To reduce the influence of these sources of bias, we have presented in [3] a new algorithm, called continuous STAPLE, to estimate a reference standard from a dataset of registered vector images. This algorithm is based on an Expectation Maximization algorithm and is similar in principle to the STAPLE validation method [4]: the reference standard is treated as unknown data in a maximum likelihood framework. The continuous STAPLE therefore iterates over two steps in order to estimate (more details on these two steps may be found in [3]):

• the reference standard underlying the dataset of images,
• a set of parameters (bias and covariance) characterizing each particular image with respect to the reference standard.

A framework has been associated to this algorithm, based on a Kullback-Leibler divergence between the Gaussian distributions defined by each set of parameters, in order to compare the images of the dataset. This framework can then be used to detect significant differences between the images.

We present in Fig. 3 experimental results on a simulated database, showing that the reference standard obtained by continuous STAPLE, looks more accurate than the one obtained by a classical average, when some outliers are present in the dataset. The tensors in the average estimate (c,f) are indeed swollen and rotated when compared to the known reference standard.

Figure 3: Comparison of STAPLE and Log-Euclidean Mean Results. Results obtained from the whole simulated database (20 control images and 4 outliers) (a): Reference noiseless image (zoom in image (d)) ; (b): Log-Euclidean mean result (zoom in image (e)) ; (c): STAPLE reference standard (zoom in image (f)).

(a)	(b)	(c)
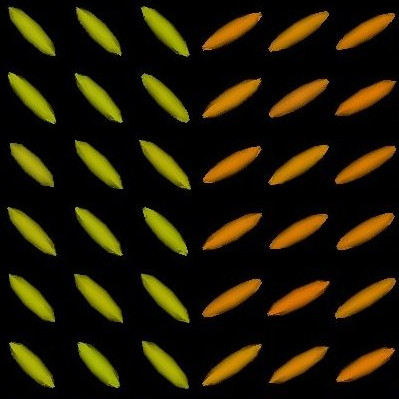(d)	(e)	(f)

Moreover, we have shown in [3] that our comparison framework was able to detect differences in these simulated experiments. We have then applied this framework to the multiple sclerosis patients, showing significant differences in the lesions regions and in their vicinity, confirming the results obtained in the previous section.

We believe that many other applications exist for this algorithm. As it can use general vector images as an input, it could be used on non linear transformations or DT images. Another potential application would be the study of the Jacobians of transformations for the detection of abnormal anatomy.

Bibliography

1. Log-Euclidean metrics for fast and simple calculus on diffusion tensors
   V. Arsigny, P. Fillard, X. Pennec, and N. Ayache.
   Magnetic Resonance in Medicine, 56(2):411-421, August 2006.
2. Detection of DTI White Matter Abnormalities in Multiple Sclerosis Patients
   O. Commowick, P. Fillard, O. Clatz and S. K. Warfield.
   In Proceedings of the 11th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI'08), Part I, volume 5241 of LNCS, pages 975-982, September 2008.
3. A Continuous STAPLE for Scalar, Vector and Tensor Images: An Application to DTI Analysis
   O. Commowick and S. K. Warfield.
   IEEE Transactions on Medical Imaging, 28(6):838-846, June 2009.
4. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation.
   S.K. Warfield, K.H. Zou and W.M. Wells.
   IEEE Transactions on Medical Imaging, 23(7):903-921, 2004.