The registration of medical images is in general a difficult problem. Numerous methods have been devised to address this problem. Rigid and affine transformations are widely used to recover global deformations, e.g. for intra-patient registration. However, they do not cope with local deformations.

Other types of transformations have therefore been developed, called non-rigid. These can be split into two classes. First, parametric transformations can be a linear combination of radial basis functions or B-Splines. These transformations can have an arbitrary number of degrees of freedom. However, defining specific areas having a common behavior can be very complicated. The second class, called dense transformations has the highest number of degrees of freedom, as it defines one displacement vector per voxel. These non-rigid methods can cope with local deformations. However, they may have too many degrees of freedom, resulting in local irregularities in the contours of structures.

We would prefer to use a transformation with few degrees of freedom for each structure. Following this idea, several approaches have already been proposed in the literature. Unfortunately, they either are quite computationally expensive and their use restricted to 2D so far, or have been specifically designed for one application.

We have introduced in [1,2] an efficient and general framework for multi-affine registration. We parameterize the transformation by a finite number \( N \) of affine components. Precisely, each component consists of an affine transformation \( A_i \) and of a non-negative weight function \( w_i(x) \) which gives the influence of the i-th component at point \( x \).

For all the intermediate interpolations, we obtain the global transformation from the weighted components using a simple fusion of the components:

This transformation is smooth, but not invertible in general. To remedy this, we use the recently proposed log-Euclidean polyaffine framework [3] at the end of the algorithm to ensure an invertible transformation.

We introduced also in this article a novel regularization approach, specific to locally affine transformations. [3] has shown that, as for diffusion tensors, taking the logarithm of affine transformations corresponds to linearizing the (curved) affine group around the identity, while conserving excellent theoretical properties (invariance with respect to inversion in particular). This allows to perform Euclidean (i.e. vectorial) operations on affine transformations via their logarithms.

This representation of affine transformations by vectors allows the direct generalization of classical vectorial regularization techniques. For example, one can define a Log-Euclidean elastic energy between affine components:

where we have \( p_{i,j}=\int_\Omega w_i(x).w_j(x)dx /\int_\Omega w_i(x)dx \), which take into account the spatial extensions of the components. Furthermore, one can define a fluid energy by regularizing the transformation corrections \( \Delta A_i \) instead of the affine transformations \( A_i \) in (2).

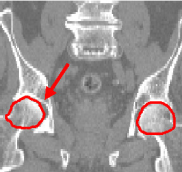
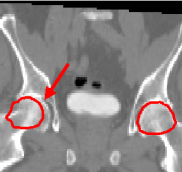
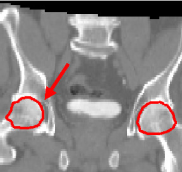
We have first evaluated the performance of our algorithm in the frame of high-precision radiotherapy planning. We want to estimate the position of soft tissues statistically, with respect to a set of landmarks established in more stable surrounding structures showing a better contrast in CT images. For that purpose, we must initially register all the patients' images to a common space. The landmarks we establish are a set of salient points in the pelvic and leg bones. For a feasibility study, we concentrate on two of them that correspond to the centers of mass of the femoral heads. The regions around these points, i.e the femoral heads themselves, are used as affine component localizations in our algorithm.

Figure 1: Registration result on the pelvis with femoral heads contours of the reference image superimposed. On the left the reference image, in the middle the floating image after a global affine registration, on right the floating image after using our algorithm.

We present here some results of the inter-patient registration process using these anatomical landmarks. All the patients' images are registered with respect to a reference image. The process consists of two stages: first, a global affine registration is performed using a block-matching algorithm, and then our algorithm is applied. In Figure 1, we can see a significant qualitative improvement on the registration result with respect to an affine transformation. Moreover, we see that the information contained in the images outside the regions used in the registration remains consistent from an anatomical point of view.

The second application of our framework is the automatic segmentation of brain critical structures for brain radiotherapy. An accurate segmentation of these structures and of the tumor allows to optimize the irradiation doses received by each structure. The method we follow consists of bringing the patient image onto an anatomical atlas. The atlas is composed of a simulated MRI of the brain and its segmentation done by an expert. The patient image is first globally positioned by an affine registration. The second step is to refine the result locally by using a non-rigid registration algorithm.

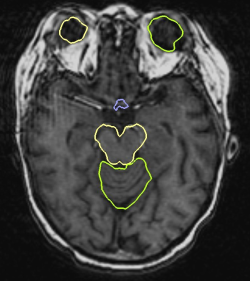
The first task to use our algorithm is to define the areas to register. In the following example, we register five critical structures: the cerebellum, the eyes, the optic chiasma and the brainstem. Thanks to our atlas, we can select the areas on which to put affine transformations in a simple manner. This was done simply by dilating the structures of the atlas. Having defined the affine areas, we first show the contribution of regularization in the registration process. We have therefore run one registration with regularization and without regularization.

Figure 2: Contribution of the regularization in the registration. From left to right: Patient image registered on the atlas without regularization (image and deformed grid) and with regularization (image and deformed grid).

This example clearly underlines the importance of the regularization. The cerebellum does not have the shape we would expect when not using regularization: there is indeed a lack of coherence between its two components yielding a result which is not consistent from an anatomical point of view. The errors also propagate to the rest of the brain. Our regularization technique solves this problem and provides consistent results all over the brain.

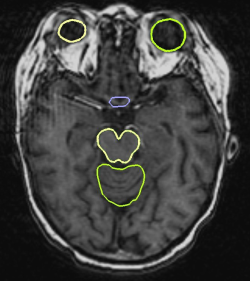
The second series of experiments consists of comparing the results of our algorithm with a dense registration algorithm. The dense method produces quite accurate segmentations (see Figure 3). However, the contours are irregular and in particular the eyes and the chiasma can have a shape that no longer looks like the real structure.

Figure 3: Qualitative comparison of the segmentation results on one patient. From left to right: Contours obtained using a dense transformation and using our new framework.

The obtained contours are much smoother than the ones obtained with a dense transformation. They are also more precise, mostly on the brainstem and the eyes. Finally, the computation time is faster (10 minutes as opposed to 40 minutes on a computer running at 3 GHz) than with the dense registration.

Bibliography

1. An Efficient Locally Affine Framework for the Smooth Registration of Anatomical Structures
   O. Commowick, V. Arsigny, A. Isambert, J. Costa, F. Dhermain, F. Bidault, P.-Y. Bondiau, N. Ayache and G. Malandain.
   Medical Image Analysis, 12(4):427-441, August 2008.
2. An Efficient Locally Affine Framework for the Registration of Anatomical Structures
   O. Commowick, V. Arsigny, J. Costa, N. Ayache, and G. Malandain.
   In Proceedings of the Third IEEE International Symposium on Biomedical Imaging (ISBI 2006), pages 478-481, April 2006.
3. A Fast and Log-Euclidean Polyaffine Framework for Locally Affine Registration
   V. Arsigny, O. Commowick, X. Pennec, and N. Ayache.
   Research Report RR-5865, INRIA Sophia-Antipolis, March 2006.