Atlas-based segmentation has been shown to be very efficient to delineate brain structures. A major localization of cancers is the head and neck region (7 % of all cancers). It would therefore be of great interest to use an anatomical atlas of this area to help the clinicians with the therapy planning.
However, on this part of the body, using an atlas built from one single image as for the brain is not adequate, since the structures to be delineated are not clearly defined. Using only one image may then introduce an undesirable bias. Building an atlas from a set of segmented images can address this issue.
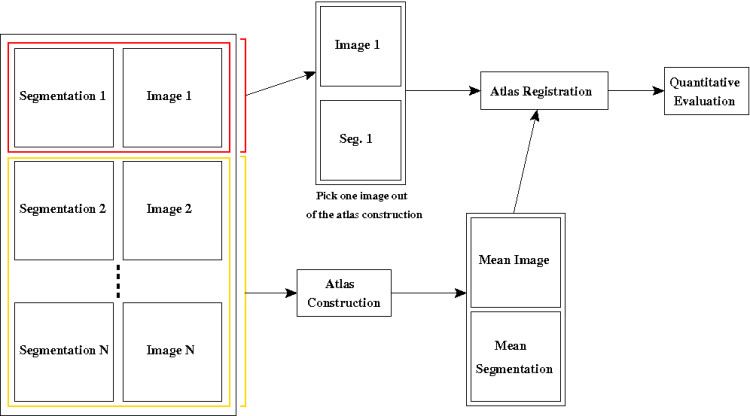
To this end, we have presented in [1] a new method to merge a database of manually delineated images into an average anatomy associated to its segmentation. The construction process is illustrated in figure 1 and can be summed up in three steps:
- Constuction of an unbiased symmetric average anatomical image,
- Apply the transformations to the manual delineations,
- Compute robust average segmentations using the STAPLE algorithm
The quality of the atlas will depend on the choice of the registration method used to fuse the images. Since the atlas is designed to delineate structures, we have presented in [2] a framework based on the evaluation of the automatic delineations obtained from the constructed atlas. This allows us to evaluate both the registration method used to build the atlas, and the one used to deform it on an individual image.
This is obtained by using a leave-one-out method illustrated on figure 2. We first leave one image out of the dataset used to build the atlas. Then, using the manual delineations of this image and the automatic segmentations obtained by the atlas registration, we can compute quantitative measures (sensitivity and specificity) of the atlas quality. By repeating this procedure on several patients of the database, we can compute mean quality measures of each atlas and determine the best one for our application.
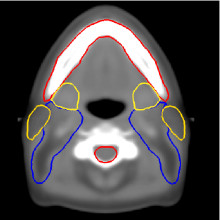
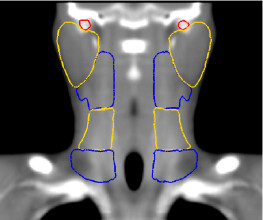
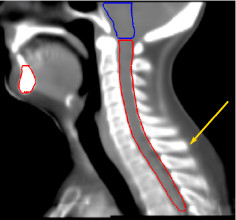
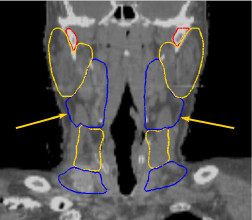
Thanks to this method, we have developed an anatomical atlas of the head and neck region, illustrated on figure 3, images (a), (b) and (c). We obtain good segmentation results (see images (d), (e), (f) in figure 3 for a qualitative view) thanks to the use of a constrained transformation (locally affine) [3] followed by a dense registration method.
 |
 |
 |
| (a) | (b) | (c) |
 |
 |
 |
| (d) | (e) | (f) |
Bibliography
-
Atlas-Based Delineation of Lymph Node Levels in Head and Neck Computed Tomography Images
O. Commowick, V. Grégoire and G. Malandain.
Radiotherapy Oncology, 87(2):281-289, May 2008.

-
Evaluation of Atlas Construction Strategies in the Context of Radiotherapy Planning
O. Commowick and G. Malandain.
In Proceedings of the SA2PM Workshop (From Statistical Atlases to Personalized Models), held in conjunction with MICCAI '06, October 2006.
-
An Efficient Locally Affine Framework for the Smooth Registration of Anatomical Structures
O. Commowick, V. Arsigny, A. Isambert, J. Costa, F. Dhermain, F. Bidault, P.-Y. Bondiau, N. Ayache and G. Malandain.
Medical Image Analysis, 12(4):427-441, August 2008.